København, august 2020
CABA Capitals Volatilitets Mindset

Kristian Myrup Pedersen
kmp@cabacapital.dk
Indledning
Der er mange forskellige tilgange til at investere, og der er næppe én tilgang, som til alle tider gør sig bedre end alle andre. Derfor er det vores overbevisning, at man som investor står sig godt ved at udvikle en velassorteret værktøjskasse med mentale investeringsmodeller, som understøtter og supplerer hinanden.
Formålet med dette notat er udbrede kendskabet til ét af vores værktøjer i CABA Capital, nemlig vores Volatilitets Mindset. Det er udviklet af CABA Capital med udgangspunkt i en kombination af vores egne praktiske investeringserfaringer og Benoit Mandelbrots teoretiske principper for finansiel modellering[1]. Volatilitets Mindsettet er en struktureret kondensering af vores dybtliggende antagelser, metoder og overbevisninger om, hvordan man bedst muligt arbejder aktivt med investeringer i en usikker verden, hvor markederne i nogle perioder udvikler sig stille og roligt og i andre perioder vildt og voldsomt.
I notatet starter vi med at introducere den overordnede investeringsfilosofi bag vores obligationsbaserede hedgefond, CABA Hedge. Vi vil i notatet tage udgangspunkt i fonden for at gøre det så praktisk relevant som muligt. Selvom vi tager udgangspunkt i vores hedgefond, kan Volatilitets Mindsettet let overføres på andre aktivklasser, herunder aktier, kreditobligationer og valuta. Med investeringsfilosofien på plads er vi klar til at åbne op for mindsettet, herunder hvordan vi konceptuelt arbejder med det ift. både investeringer og risikostyring. Derefter dykker vi ned i selve modellen bag mindsettet og viser, at den understøttes af empirisk analyse (OBS: afsnittet er mest for teknisk interesserede læsere, og det kan derfor eventuelt blot læses kursorisk). Afslutningsvis illustrerer vi brugen af mindsettet med en konkret handel fra CABA Hedge.
[1] Benoit Mandelbrot, som er faderen til den matematiske disciplin fraktal geometri, har i bogen ”The (Mis)Behaviour of Markets – A Fractal View of Risk, Ruin and Reward” overført principperne bag fraktal geometri til finansiel modellering.
Investeringsfilosofi
Der er som sagt mange forskellige tilgange til at investere, og alt efter formålet kan de opdeles og beskrives på mange forskellige måder. Den allermest simple, og den som vi vil tage udgangspunkt i her, er at opdele investeringstilgange i enten beta-strategier eller alpha-strategier, jf. nedenstående tabel.
Tabel 1: Beta-strategier vs. Alpha-strategier

Kilde: CABA Capital
I CABA Hedge kombinerer vi de to investeringstilgange i den forstand, at vi søger at opnå en afkastmedvind fra beta-strategier, samtidig med at vi søger at udnytte alphamuligheder på opportunistisk basis. Det skyldes, at vi på den ene side har den overbevisning, at markederne i det store hele er effektive, og at man derfor får en belønning for at høste risikopræmier over tid. På den anden side er det dog samtidig vores overbevisning, at realkreditmarkederne i Skandinavien ikke er 100% effektive, og at vi med vores erfaring og lokalkendskab kan udnytte disse inefficiencer til at skabe alpha på toppen af beta-strategierne.
Som nævnt tager beskrivelsen af mindsettet udgangspunkt i vores obligationsbaserede hedgefond, CABA Hedge, og vi vil derfor kort behandle de risikopræmier, som vi har eksponering mod i fonden. I CABA Hedge udnytter vi det forhold, at lavrisiko risikopræmier har en tendens til at give attraktive risikojusterede afkast, dog uden at de nødvendigvis er attraktive i absolutte termer. Derfor isolerer vi disse risikopræmier og gearer dem op, således at det forventede afkast bliver attraktivt i både relative og absolutte termer. Helt konkret kan vi eksempelvis købe realkreditobligationer og afdække renterisikoen ved at sælge statsobligationer og på den måde isolere renteforskellen mellem dem uden at have nogen renterisiko. I risikopræmiediamanten nedenfor har vi illustreret de primære risikopræmier, som vi har eksponering mod i fonden.
Figur 1: Risikopræmiediamanten
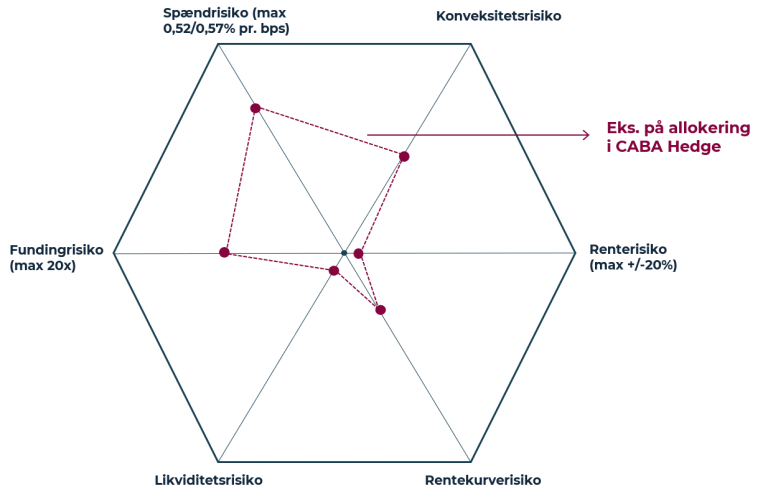
Kilde: CABA Capital
Kort fortalt har vi i diamanten to risikopræmier, som vi aktivt søger at høste over tid, nemlig spændrisiko og konveksitetsrisiko. Disse to risikopræmier giver efter vores vurdering hver især en attraktiv strukturel risikopræmie. I diamanten har vi også fire risikopræmier, vi ikke fuldstændig kan undgå, men som vi søger at mindske eksponeringen mod, nemlig renterisiko, rentekurverisiko, likviditetsrisiko og fundingrisiko.
I resten af notatet vil vi alene fokusere på de to førstnævnte risikopræmier, dvs. spændrisiko og konveksitetsrisiko, idet vores Volatilitets Mindset primært er rettet mod disse. Helt konkret bruger vi mindsettet til at hjælpe os med 1) at vurdere, hvor attraktive risikopræmierne er på et givet tidspunkt, 2) hvordan vi skal skalere vores eksponering mod dem, og 3) hvordan vi skal styre risikoen omring dem.
Volatilitets Mindsettet
Mindsettet tager sit konceptuelle udspring i det fænomen, at markederne i nogle perioder udvikler sig stille og roligt og i andre perioder vildt og voldsomt. I Benoit Mandelbrots finansielle modellering sondrer han mellem kalendertid og markedstid. Sondringen har både en intuitiv fortolkning, som vi vil arbejde videre med nedenfor, og en række modeltekniske implikationer, som vi vil arbejde videre med i næste afsnit.
Den intuitive fortolkning af sondringen mellem kalendertid og markedstid er, at selvom vi normalt fokuserer på kalenderdage alene, så ved enhver investor jo egentlig godt, at markedstiden nogle gange går meget hurtigere end kalendertiden. Dage kan føles som måneder, og måneder kan føles som år. Der kommer nogle gange så meget ny information, at man slet ikke kan nå at følge med. Det er typisk sammenfaldende med perioder med større kursudsving end normalt. Foråret 2020 var et ekstremt eksempel på dette. Alting stod i Coronaens tegn, og markedstiden gik måske hurtigere end nogensinde før. Hver dag udspillede der sig vilde begivenheder, som hver især krævede dybe analyser, og de store aktieindeks svingede med 5-10% på daglig basis. Andre dage går markedstiden omvendt gabende langsomt. De dage kæmper man for at holde sig vågen foran skærmene, og uanset hvor meget man stirrer på kurserne, sker der bare intet.
Det store spørgsmål er jo selvfølgelig, hvordan man i praksis vurderer, om den nære fremtid vil byde på ”stille tider” eller ”vilde tider”. Vi arbejder med mange forskellige inputs for at vurdere, hvad fremtiden kan tænkes at bringe, herunder aktuelle begivenheder, makroøkonomi, centralbank og investoradfærd. Erfaring spiller en stor rolle her. Det er tillokkende at sætte vurderingen på formel, men eftersom den har karakter af en blanding af kunst og videnskab, lader det sig ikke gøre i praksis. Vi vil ikke komme det nærmere her, men i sidste del af notatet giver vi et eksempel på, hvordan man kan gøre det i praksis.
Der er altid et trade-off mellem afkast og risiko. Vores Volatilitets Mindset hjælper os med at vægte de to hensyn op imod hinanden. Ved udsigt til ”stille tider” vægter vi afkast højere end normalt, og ved udsigt til ”vilde tider” vægter vi risiko højere end normalt. Kernen i mindsettet er skitseret i tabellen nedenfor.
Tabel 2: Kernen i CABA Capitals Volatilitets Mindset
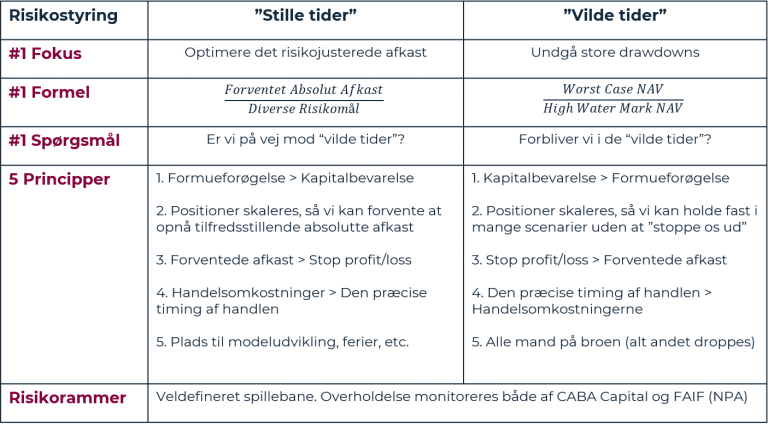
Kilde: CABA Capital
I CABA Hedge arbejder vi primært med investeringer i skandinaviske realkreditobligationer, og som sådan er vores analytiske værktøjskasse baseret på klassiske værktøjer fra obligationsanalysen. Skåret ind til benet kan disse værktøjer opdeles i 1) Tidsserieanalyse, 2) Tværsnitsanalyse, og 3) Flowanalyse. I stedet for altid at bruge værktøjerne på samme måde har vi med Volatilitets Mindsettet udviklet en guidance til, hvordan man med fordel kan bruge dem forskelligt i henholdsvis ”stille tider” og ”vilde tider”, jf. nedenfor.
Tabel 3: Værktøjskassen

Kilde: CABA Capital
Tidsserieanalyse kan blandt andet bruges til at sammenligne risikopræmier, såsom belønning for spændrisiko og konveksitetsrisiko, med sig selv over tid. I ”stille tider” kan man således bruge dette værktøj som input i vurderingen af, om en given risikopræmie er attraktiv eller ej. Hvis risikopræmien eksempelvis ligger i den høje ende af sit eget historiske range, vil risikopræmien alt-andet-lige være mere attraktiv, end hvis den ligger i den lave ende. I ”vilde tider” kan man blandt andet bruge værktøjet til at få et indtryk af, hvor meget risikopræmien kan variere i ekstreme perioder ved at betragte de største historiske stigninger i perioden. Det kan være et input i vurderingen af timing og skalering af eksponeringen mod risikopræmien.
Tværsnitsanalyse kan blandt andet bruges til at sammenligne aktuelle risikopræmier med hinanden. I ”stille tider” kan man således bruge værktøjet at sammenligne risikopræmier på tværs af investeringsuniverset, eksempelvis spændrisikopræmierne på korte og lange Flex’ere. I ”vilde tider” kan værktøjet også bruges til at sammenligne risikopræmierne inden for investeringsuniverset med risikopræmier uden for investeringsuniverset, herunder risikopræmierne på aktier og kreditobligationer. Sidstnævnte skyldes, at man i ”vilde tider” i højere grad end normalt kan udnytte viden fra andre markeder. Hvis f.eks. aktiemarkedet falder kraftigt, vil ligevægtsrisikopræmierne på realkreditobligationer alt-andet-lige stige, men der er flere historiske eksempler på, at ligevægtsdannelsen af risikopræmier på tværs af markeder ikke sker simultant.
Flowanalyse kan blandt andet bruges til at positionere sig til at kunne profitere af fremtidige udbuds- og efterspørgselseffekter. I ”stille tider” kan flowanalyse eksempelvis bruges til at vurdere, om man skal købe konverterbare realkreditobligationer ”nu og her”, eller om man hellere skal vente på perioder med stor udstedelse i forbindelse med låneomlægninger. I ”vilde tider” kan flowanalyse bruges til at vurdere, om der kan opstå såkaldte tipping points, hvor andre markedsdeltagere kan blive ”tvunget” til at likvidere positioner med deraf følgende nedadgående prispres. Det ses typisk ved massive rentestigninger og under store kriser.
Modellen bag Mindsettet
I dette afsnit viser vi, at der er empirisk belæg for at arbejde med sondringen mellem ”stille tider” og ”vilde tider” på realkreditmarkedet. Afsnittet udgør det empiriske fundament for mindsettet.
I den finansielle sektor oplever man ofte det paradoks, at alle er enige om, at afkast på finansielle aktiver ikke følger normalfordelingen på grund af både asymmetri og fede haler. Alligevel er normalfordelingen hjørnestenen i den ”moderne porteføljeteori”, ligesom praktikere ofte anvender risiko- og performancemål fra den normalfordelte verden, herunder standardafvigelse, Sharpe ratio og mange varianter af Value-at-Risk. Forklaringen bag paradokset er nok, at normalfordelingen er så let og elegant at arbejde med, at den ofte vinder over de mere besværlige alternativer, også selvom de måtte være mere retvisende. Lad os illustrere problematikken ved at betragte de daglige ændringer i realkreditspændet på danske 30-årige konverterbare obligationer igennem de seneste 20 år (trendjusteret), jf. figuren nedenfor.
Figur 2: Histogram over daglige ændringer i realkreditspænd (hele fordelingen)
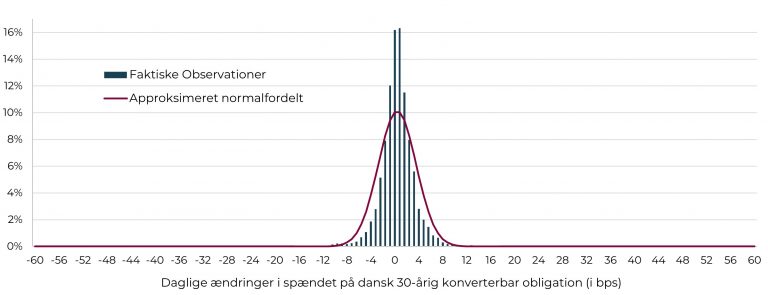
Kilde: CABA Capital og Nordea Analytics
Ved første øjekast fremstår problematikken måske ikke så tydelig, udover at de faktiske observationer umiddelbart er for centrerede omkring middelværdien på nul. Hvis man zoomer ind på den nederste del af histogrammet, bliver det dog tydeligt, at centreringen modsvares af ekstreme outliers, jf. figuren nedenfor.
Figur 3: Histogram over daglige ændringer i realkreditspænd (fokus på halerne)
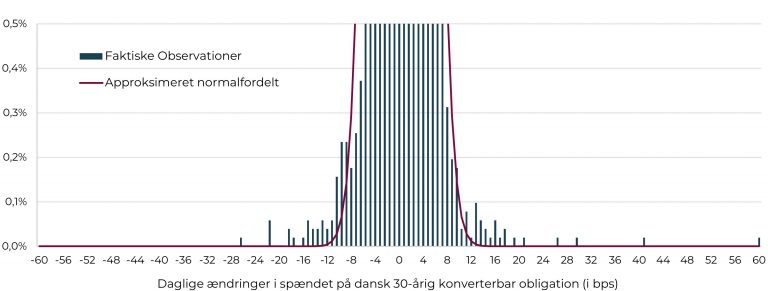
Kilde: CABA Capital og Nordea Analytics
Vi kan få lidt mere indsigt i, hvordan de faktiske observationer adskiller sig fra den approksimeret normalfordeling ved at sammenligne de faktiske daglige ændringer i realkreditspændet over tid med en simuleret tidsserie over daglige ændringer approksimeret fra normalfordelingen, jf. nedenstående.
Figur 4: Tidsserie med faktiske ændringer i realkreditspænd (bps)
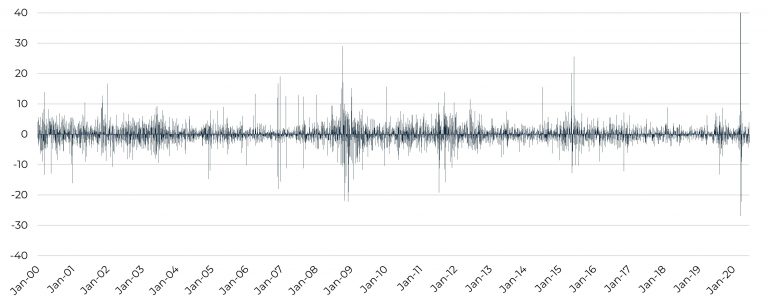
Kilde: CABA Capital og Nordea Analytics
Figur 5: Tidsserie med normalfordelte ændringer i realkreditspænd (bps)
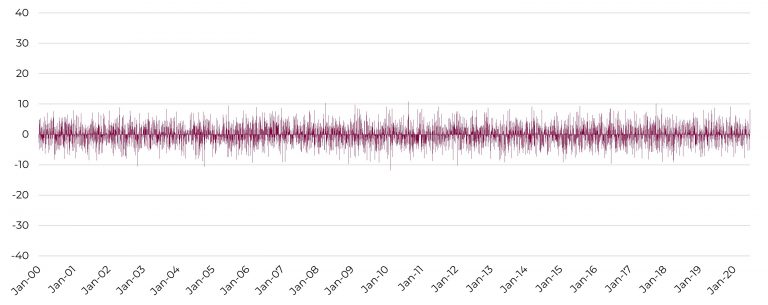
Kilde: CABA Capital og Nordea Analytics
Som det fremgår af figurerne, er de faktiske daglige ændringer meget mere uens fordelt end de normalfordelte. Der er perioder, hvor de faktiske ændringer er meget mindre end i normalfordelingen, og perioder hvor de er meget større. Dette turbulente fænomen kan beskrives på den måde, at volatiliteten i sig selv er stokastisk og følger et tidsafhængigt mønster med klynger af henholdsvis lav og høj volatilitet. Fænomenet findes i øvrigt på tværs af finansielle aktiver såsom aktier, kreditobligationer og valuta.
Der er mange måder at modellere stokastisk volatilitet på, men vi har valgt at bruge principperne bag Benoit Mandelbrots fraktal geometriske tilgang [2]. Det skyldes, at modellering baseret på disse principper er intuitiv, efterlader os med mange frihedsgrader i selve modelleringen og giver virkelighedsnære resultater. Hans tilgang kan – i kombination med normalfordelingen – generere afkastfordelinger med fede haler. Vi har selv videreudviklet tilgangen, så den også kan skabe både asymmetrien og den ustabile samvariation (mellem realkreditspænd og renter), som vi observerer i virkelighedens verden. Det vender vi tilbage til senere.
Den fraktale geometri kan bruges til at modellere markedstiden som funktion af kalendertiden [3]. Man kan tænke på modelleringen som en multiplikativ kaskade, men i bund og grund handler det blot om at finde en stokastisk proces, som i sidste ende kan generere det ønskede outcome i form af en virkelighedsnær fordeling for ændringerne i en given finansiel variabel. I figuren nedenfor ses et eksempel på resultaterne af vores model for markedstid for realkreditspænd. På y-aksen betyder tal over 1, at markedstiden går hurtigere end kalendertiden, og jo højere tallet er, jo hurtigere går markedstiden relativt til kalendertiden. Der vil i øvrigt per konstruktion i gennemsnit gå én markedsdag pr. kalenderdag over hele perioden.
[2] Dette er ækvivalent til at modellere stokastisk volatilitet. Med andre ord følger markedstid og volatilitet samme tidsafhængige mønster.
[3] Fraktal geometri blev oprindeligt brugt til at beskrive ”selv-similære” mønstre i naturen. Man kan f.eks. bruge fraktal geometri til at beskrive geometrien af et træ, som bliver ved med at forgrene sig (stamme, gren, kvist). Grunden til at man kan bruge samme princip på finansielle data er, at disses ændringer har en tendens til at følge samme underliggende mønster, bare på forskellige tidsskalaer (år, måned, uge).
Figur 6: Eksempel fra vores markedstidsmodel for realkreditspænd
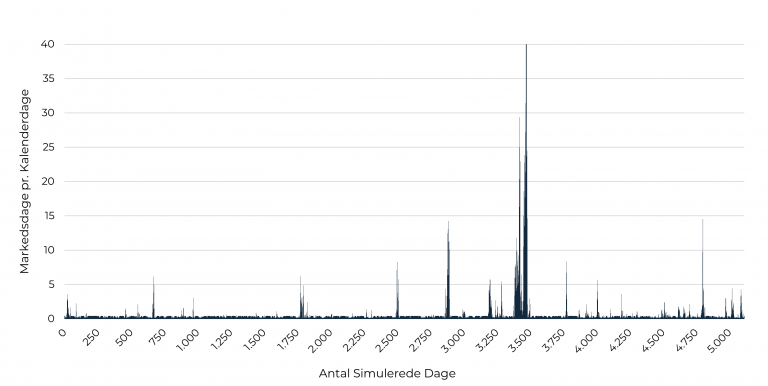
Kilde: CABA Capital
Det smarte ved denne modelleringstilgang er, at man ved at skalere markedstiden med denne stokastiske proces kan simulere daglige ændringer i realkreditspænd, som statistisk set stemmer godt overens med de faktiske observationer. Dette er illustreret i figurer 7 og 8 nedenfor, som kan sammenholdes med figur 3 og 4.
Figur 7: Histogram: Daglige ændringer i realkreditspænd (bps)
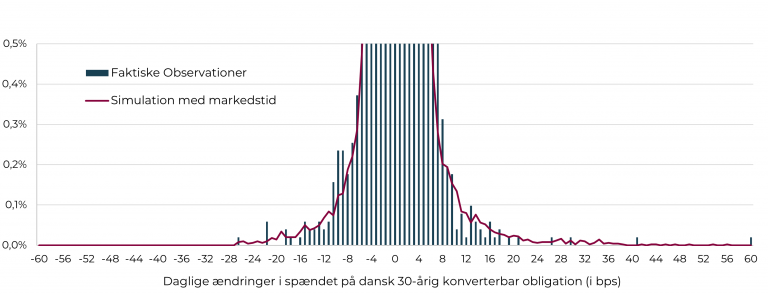
Kilde: CABA Capital
Figur 8: Simulerede ændringer i realkreditspænd (bps)
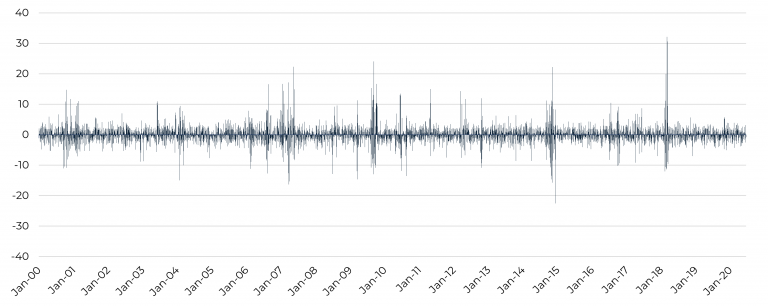
Kilde: CABA Capital
På baggrund af ovenstående figurer kan det visuelt konstateres, at modellen kan bruges til at simulere et både virkelighedsnært histogram og volatilitetsmønster. Dette understøttes af, at fordelingen af de simulerede daglige ændringer statistisk set stemmer fint overens med den faktiske fordeling, når man betragter de fire momenter, dvs. middelværdi (0), standardafvigelse (3), skævhed (2) og kurtosis (40). Dermed konkluderes det, at der er empirisk belæg for at arbejde med en sondring mellem ”stille tider” og ”vilde tider” på realkreditmarkedet. Samlet set illustrerer analysen det empiriske fundament for mindsettet.
Dette er imidlertid blot starten på en større modelrejse, som vi af pladshensyn ikke vil fuldføre her. Det skal for fuldstændighedens skyld blot nævnes, at man kan fortsætte rejsen med også at bygge en model for rentebevægelser. Man kan så efterfølgende smelte modellerne sammen. Det viser sig nemlig, at renter og realkreditspænd samvarierer i tiden i den forstand, at når markedstiden går hurtigt på det ene marked, tenderer tiden også til at gå hurtigt på det andet marked. Vores samlede tidsmodel er illustreret nedenfor.
Figur 9: Eksempel fra vores markedstidsmodel for både realkreditspænd og renter.
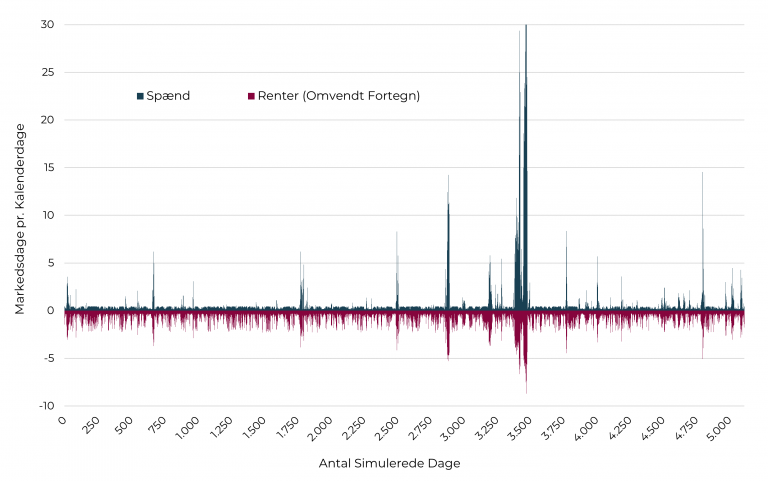
Kilde: CABA Capital
Med udgangspunkt i markedstidsmodellen kan man blandt andet lave virkelighedsnære Value-at-Risk beregninger, hvilket yderligere styrker anvendelsen af modellen i praksis.
Hvis du er nysgerrig efter at få et dybere indblik i, hvordan den samlede markedstidsmodel er konstrueret, og hvad den kan bruges til i praksis, er du meget velkommen til at kontakte vores Chief Product Manager, Kristian Myrup Pedersen (+45 30 10 22 58 / kmp@cabacapital.dk) med henblik på at høre mere.
Mindsettet i praksis
I dette afsnit vil vi illustrere, hvordan man i praksis kan bruge Volatilitets Mindsettet med udgangspunkt i en konkret handel fra CABA Hedge. Eksemplet er fra Coronakrisen, hvor porteføljemanagerne i CABA Hedge i ugerne op til de massive kursfald på dansk realkredit (i midten af marts) etablerede en short position i 30-årige konverterbare obligationer [4]. Det skal understreges, at der lå mange flere tanker bag handlen, end dem vi kan komme ind på her, og at handlen også skal ses i lyset af de andre positioner i fonden.
Lad os starte med at sammenholde det efterhånden velkendte volatilitetsmønster over daglige ændringer i realkreditspænd med et tilsvarende mønster for aktier. Som det fremgår af figuren nedenfor, følger begge aktivklasser samme mønster med klynger af henholdsvis lav og høj volatilitet. Det fremgår også, at der er en tendens til, at perioder med ekstraordinært stor volatilitet samvarierer over tid, eksempelvis under Finanskrisen i 2008/2009, Eurogældskrisen i 2011 og senest Coronakrisen i 2020. Det er dog ikke altid tilfældet, og det ses tydeligt under ”Realkreditkrisen i 2015”, hvor realkreditspændene kørte ud efter massive rentestigninger. I den periode var spændudvidelserne i høj grad et isoleret dansk fænomen.
[4] For fuldstændighedens skyld skal det nævnes, at vores erfaringer fra Coronakrisen inspirerede os til at formalisere mindsettet. Når det er sagt, så er mindsettet, som tidligere nævnt, en struktureret kondensering af vores dybtliggende antagelser, metoder og overbevisninger om, hvordan man bedst muligt arbejder aktivt med investeringer i en usikker verden, og som sådan var mindsettet med til at påvirke beslutningerne under krisen.
Figur 10: Daglige volatilitetsmønstre for realkreditspænd og aktier
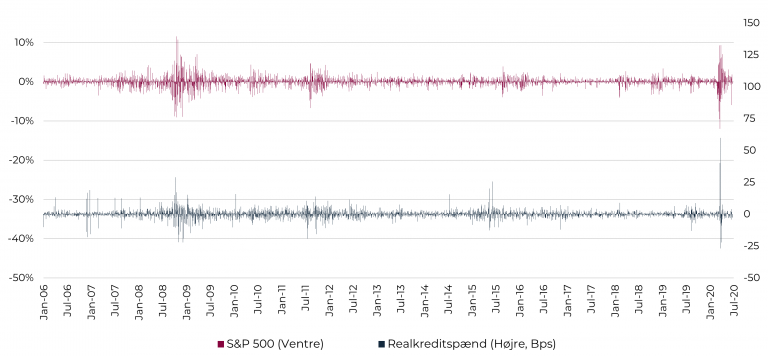
Kilde: CABA Capital, Nordea Analytics og Bloomberg
Det fremgår også af ovenstående figur, at Coronakrisen (med daglige kurstab og spændudvidelser som målestok) var dybere end finanskrisen. De daglige tab på aktiemarkedet slog historiske rekorder, ligesom realkreditspændudvidelserne kørte historisk meget ud. Det var i sandhed ”vilde tider” på markederne.
De ”vilde tider” på markederne var dog ikke fuldstændig sammenfaldende. Som det fremgår af nedenstående figur, hvor vi har zoomet ind på udviklingen i 2020, begyndte de ”vilde tider” på aktiemarkedet tre uger, før de ramte realkreditmarkedet.
Figur 11: De "vilde tider" på aktiemarkedet var tre uger foran realkreditmarkedet
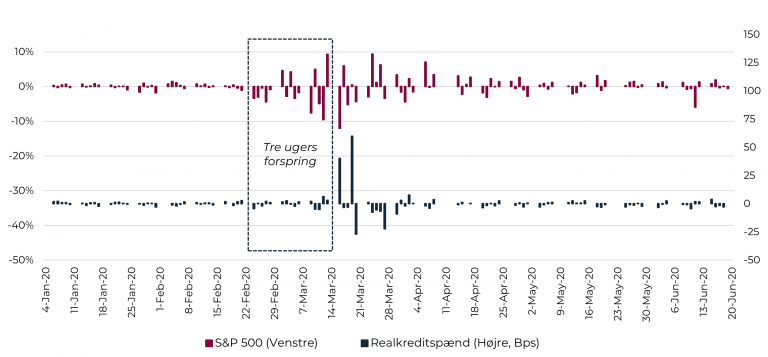
Kilde: CABA Capital, Nordea Analytics og Bloomberg
Aktieforspringet medvirkede til at porteføljemanagerne for CABA Hedge, ved at følge Coronasituationen tæt og sammenholde udviklingen på realkreditmarkedet med andre markeder, fik mulighed for at tilpasse positionerne til en periode med forøget sandsynlighed for ”vilde tider” på realkreditmarked. I denne tre ugers periode opbyggede de den omtalte short position i konverterbare obligationer, og valget af denne position skyldtes blandet andet, at den netop giver gode afkastmuligheder i ekstreme scenarier. Positionen gav efterfølgende et pænt afkast (se eventuelt rapportering for marts her). Ovenstående illustration viser, hvordan vores Volatilitets Mindset kan inspirere i praksis, om end det jo selvfølgelig kun skal være ét ud af mange redskaber i værktøjskassen.
Afslutning
Det er vores håb, at vi med vores Volatilitets Mindset har inspireret dig – enten til at udbygge din egen værktøjskasse eller til at høre mere om CABA Hedge. Du er velkommen til at kontakte os herom på info@cabacapital.dk
Disclaimer: Dette er markedsføringsmateriale. Der henvises til investoroplysning for CABA Hedge KL og til KIID-dokumentet, inden der træffes en endelig investeringsbeslutning. Materialet er produceret af Fondsmæglerselskabet CABA Capital A/S (”CABA Capital”) med det formål at orientere. Oplysningerne heri udgør ikke et tilbud eller en opfordring om at købe eller sælge investeringer, og oplysningerne skal ikke betragtes som værende investeringsrådgivning. CABA Capital og dets tilknyttede selskaber yder ikke skatte-, juridisk- eller regnskabsrådgivning. Dette materiale er ikke beregnet til at yde og bør ikke påberåbes for skatterådgivning, juridisk eller regnskabsrådgivning. Du bør konsultere dine egne skatterådgivere, juridiske og regnskabsrådgivere, inden du foretager en transaktion. Alle investeringer i værdipapirer indebærer risici, som blandt andet inkluderer risikoen for negativ eller uventet markeds-, finans- eller politisk udvikling og, i internationale transaktioner, valutarisiko. På grund af sådanne risici kan værdien af værdipapirer gå op såvel som ned. Gearing kan forstærke udsving i afkast sammenlignet med markedet. Historiske resultater udgør ikke nogen forudsigelse om fremtidigt afkast. Fremtidige resultater er skattepligtige og afhænger af den enkelte investors personlige situation, hvilket også kan ændre sig i fremtiden. CABA Capital har taget omhu for at sikre, at oplysningerne heri er komplette og korrekte. CABA Capital garanterer dog ikke, at dette er tilfældet og påtager sig intet ansvar for fejl, stavefejl eller mangler.
